Exploring the Core of Binary Operations

Binary operations form a fundamental part of mathematics and computer science. They are essential in various fields, from algebra to programming, and understanding them can unlock deeper insights into how systems work. This article will guide you through the core concepts of binary operations, providing clear explanations, practical examples, and useful tips to grasp their significance.

Understanding Binary Operations in Depth

Binary operations involve combining two elements from a set to produce another element of the same set. This concept is crucial because it defines how elements interact within mathematical structures like groups, rings, and fields. For example, addition and multiplication of numbers are common binary operations.

To understand binary operations better, consider the set of integers. When you add two integers, the result is always another integer. This closure property is a key characteristic of binary operations. Other properties to consider include associativity, commutativity, and the existence of identity elements.

• Closure: The operation on any two elements of the set results in an element still within the set.

• Associativity: Changing the grouping of operations does not change the result.

• Commutativity: Changing the order of the elements does not change the result.

• Identity element: There exists an element in the set that, when combined with any other element, leaves it unchanged.

  
  

Understanding these properties helps in identifying and working with binary operations in various contexts.

Mathematical equation illustrating binary operation properties

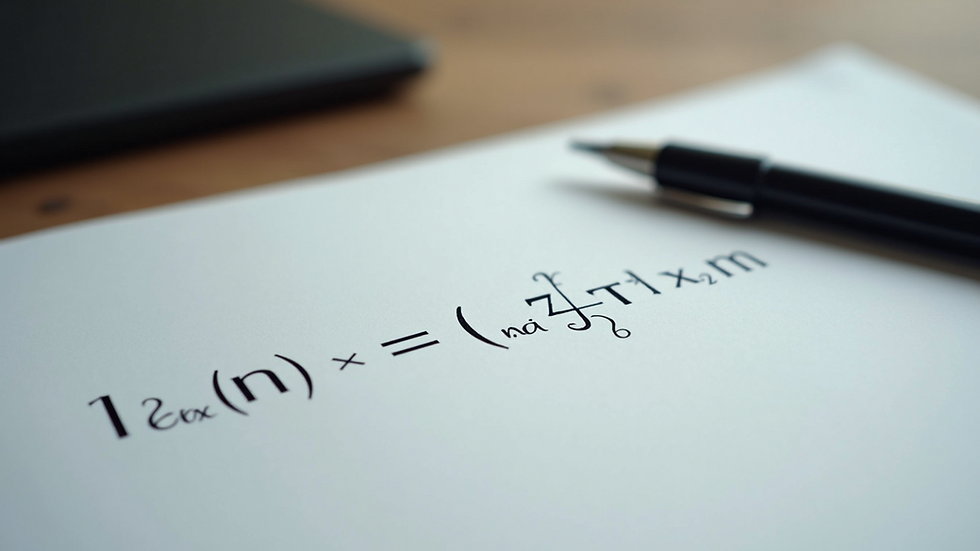
The Role of Binary Operations in Computer Science

In computer science, binary operations are foundational to algorithms, data structures, and programming languages. They enable computers to perform calculations, manipulate data, and execute logical decisions efficiently.

For instance, bitwise operations such as AND, OR, XOR, and NOT are binary operations applied to binary digits (bits). These operations are essential in low-level programming, cryptography, and error detection.

Moreover, binary operations are used in defining functions and procedures that take two inputs and return a single output. Understanding these operations allows programmers to optimize code and solve complex problems effectively.

Practical applications include:

1. Arithmetic calculations - addition, subtraction, multiplication, division.

2. Logical operations - AND, OR, XOR for decision-making.

3. Data manipulation - shifting bits, masking, and toggling bits.

   
   

Computer motherboard illustrating hardware-level binary operations

What is a binary operation?

A binary operation is a rule for combining two elements from a set to produce a third element from the same set. Formally, if you have a set S, a binary operation on S is a function that takes any two elements a and b from S and returns another element c in S, denoted as a b = c.

For example, consider the set of real numbers with the operation of addition. Adding any two real numbers results in another real number, so addition is a binary operation on the set of real numbers.

Binary operations are not limited to numbers. They can be defined on other sets, such as matrices, functions, or even strings, as long as the operation combines two elements to produce a third element within the same set.

Understanding this concept is crucial for exploring more advanced mathematical structures and computer science applications.

Whiteboard showing examples of binary operations

Examples of Binary Operations in Everyday Life

Binary operations are not just abstract concepts; they appear in everyday situations and practical tasks. Here are some relatable examples:

• Combining ingredients in cooking: Mixing two ingredients to create a new mixture.

• Merging two lists: Combining two lists of items into one.

• Social interactions: Two people shaking hands can be seen as a binary operation producing a social connection.

  
  

In mathematics and computing, these examples translate into operations like addition, concatenation, or logical conjunction. Recognising binary operations in daily life helps in understanding their importance and application.

To practice, try identifying binary operations in your daily activities or in problems you encounter. This approach will deepen your comprehension and make abstract concepts more tangible.

Practical Tips for Mastering Binary Operations

To effectively learn and apply binary operations, consider the following recommendations:

• Start with simple sets: Work with familiar sets like integers or real numbers before moving to complex structures.

• Practice properties: Verify closure, associativity, and commutativity for different operations.

• Use visual aids: Diagrams and tables can help illustrate how operations work.

• Apply in programming: Experiment with binary operations in coding exercises, especially bitwise operations.

• Explore real-world problems: Relate binary operations to practical scenarios to enhance understanding.

  
  

By following these tips, you can build a strong foundation in binary operations and apply this knowledge across various disciplines.

For a deeper dive into binary operations, including detailed examples and exercises, visit the linked resource.

Understanding the core of binary operations opens doors to advanced mathematical reasoning and efficient computing techniques. Embrace the challenge and explore the fascinating world of binary operations to enhance your analytical skills and problem-solving abilities.